What are integrodifference equations?
Integrodifference equations track the density organisms from one generation to the next, based on processes of survival, reproduction, and dispersal.
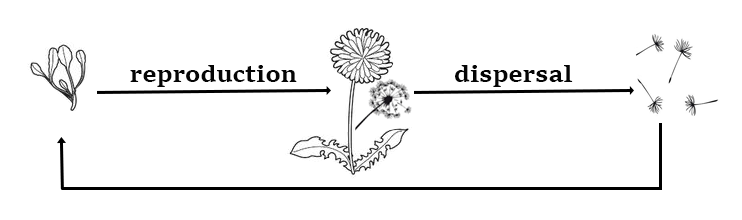
Biologically, integrodifference equations are particularly suited to model organisms whose life cycle consists of a reproduction and a dispersal phase that are separated in time and synchronized in the population. Many plant and insect species have these life-cycle characteristics.
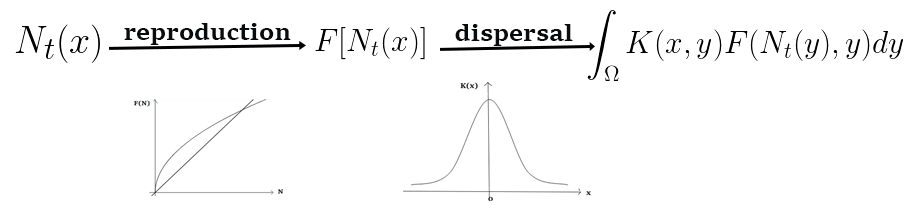
Mathematically, integrodifference equations are discrete dynamical systems on some appropriate function space, typically infinite dimensional.
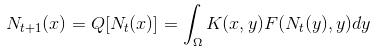
Questions, for example, from conservation ecology about the persistence and distribution of species correspond to questions of existence and stability of steady states for the equations.

Questions, for example, from invasion biology about the spatial spread of species correspond to questions about travelling waves and spreading speeds.