What are integrodifference equations?
Integrodifference equations track the density organisms from one year or generation to the next, based on processes of survival, reproduction, and dispersal. Hence, time is discrete and space is continuous.
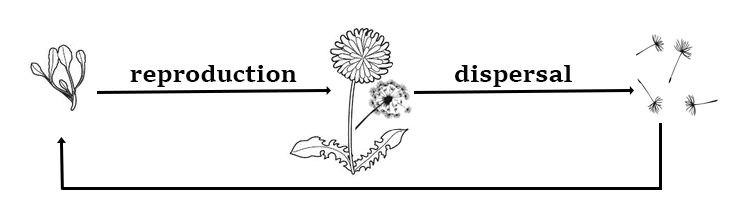
Biologically, integrodifference equations are particularly suited to model organisms whose life cycle consists of a reproduction and a dispersal phase that are separated in time and synchronized in the population. Many plant and insect species have these life-cycle characteristics.
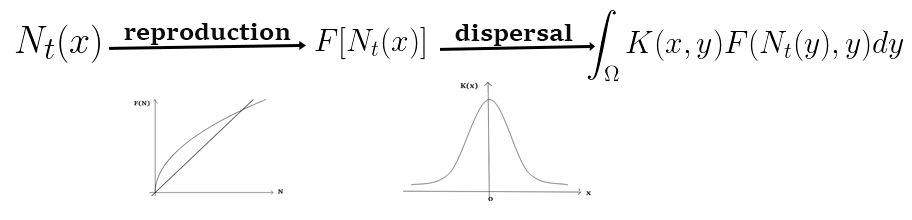
Mathematically, integrodifference equations are discrete dynamical systems on some appropriate function space, which is typically infinite dimensional since it represents densities in continuous physical space Ω.
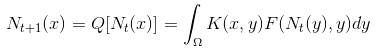
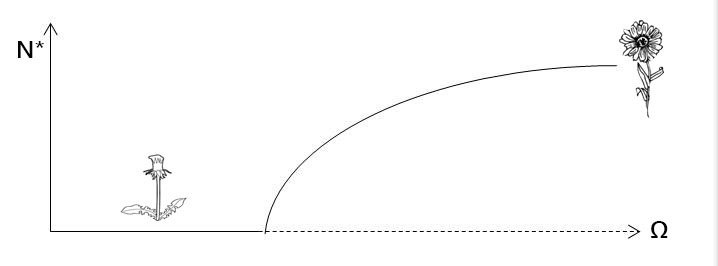
For example, questions from population biology and conservation about the persistence and distribution of species correspond to questions of existence and stability of steady states, N*, for the equations.
For example, questions from invasion biology about the spatial spread of species correspond to questions about travelling waves and spreading speeds.
Entering the world of integrodifference equations
The foundational paper on integrodifference equations on bounded domains is by Kot and Schaffer (1986). For questions of spread, we recommend the paper by Kot, Lewis and van den Driessche (1996) or the review paper by Kot (2003).
Building on these foundations, research advanced and included aspects of complex life history, spatial and temporal heterogeneity, stochasticity and many other topics. An (almost) complete list of publications on integrodifference equations is here.
Related Models
We consider the continuous variable to represent physical space. Other applications consider age, size or other traits. The resulting integral projection models are closely related to integrodifference models but we will not consider them here.
